Publications

2025

1. 

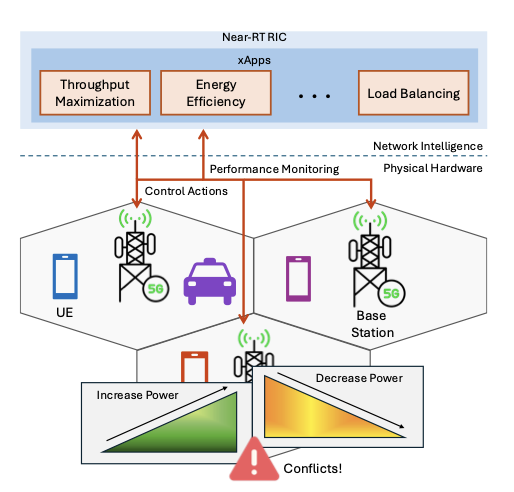   Towards xApp Conflict Evaluation with Explainable Machine Learning and Causal Inference in O-RAN

   Pragya Sharma, Shihua Sun, Shachi Deshpande, and 2 more authors

   In Proceedings of the IEEE Conference on Network Function Virtualization and Software Defined Networks (NFV-SDN) , 2025

   Best Paper Award

   Abs PDF

   The Open Radio Access Network (O-RAN) architecture enables a flexible, vendor-neutral deployment of 5G networks by disaggregating base station components and supporting third-party xApps for near real-time RAN control. However, the concurrent operation of multiple xApps can lead to conflicting control actions, which may cause network performance degradation. In this work, we propose a framework for xApp conflict management that combines explainable machine learning and causal inference to evaluate the causal relationships between RAN Control Parameters (RCPs) and Key Performance Indicators (KPIs). We use model explainability tools such as SHAP to identify RCPs that jointly affect the same KPI, signaling potential conflicts, and represent these interactions as a causal Directed Acyclic Graph (DAG). We then estimate the causal impact of each of these RCPs on their associated KPIs using metrics such as Average Treatment Effect (ATE) and Conditional Average Treatment Effect (CATE). This approach offers network operators guided insights into identifying conflicts and quantifying their impacts, enabling more informed and effective conflict resolution strategies across diverse xApp deployments.

2. 

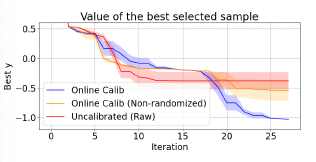   Calibrated Regression Against An Adversary Without Regret

   Shachi Deshpande, Charles Marx, and Volodymyr Kuleshov

   In Proceedings of the Forty-first Conference on Uncertainty in Artificial Intelligence , 21–25 jul 2025

   Abs PDF

   We are interested in probabilistic prediction in online settings in which data does not follow a probability distribution. Our work seeks to achieve two goals: (1) producing valid probabilities that accurately reflect model confidence; (2) ensuring that traditional notions of performance (e.g., high accuracy) still hold. We introduce online algorithms guaranteed to achieve these goals on arbitrary streams of data-points, including data chosen by an adversary. Specifically, our algorithms produce forecasts that are (1) calibrated i.e., an 80% confidence interval contains the true outcome 80% of the time-and (2) have low regret relative to a user-specified baseline model. We implement a post-hoc recalibration strategy that provably achieves these goals in regression; previous algorithms applied to classification or achieved (1) but not (2). In the context of Bayesian optimization, an online model-based decision-making task in which the data distribution shifts over time, our method yields accelerated convergence to improved optima.

2024

1. 

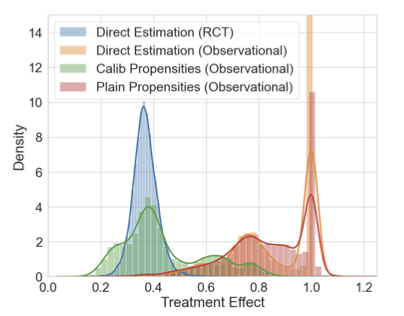   Calibrated Propensity Scores for Causal Effect Estimation

   Shachi Deshpande, and Volodymyr Kuleshov

   In Uncertainty in Artificial Intelligence (UAI) , 21–25 jul 2024

   Abs PDF

   Propensity scores are commonly used to estimate treatment effects from observational data. We argue that the probabilistic output of a learned propensity score model should be calibrated – i.e., a predictive treatment probability of 90% should correspond to 90% of individuals being assigned the treatment group – and we propose simple recalibration techniques to ensure this property. We prove that calibration is a necessary condition for unbiased treatment effect estimation when using popular inverse propensity weighted and doubly robust estimators. We derive error bounds on causal effect estimates that directly relate to the quality of uncertainties provided by the probabilistic propensity score model and show that calibration strictly improves this error bound while also avoiding extreme propensity weights. We demonstrate improved causal effect estimation with calibrated propensity scores in several tasks including high-dimensional image covariates and genome-wide association studies (GWASs). Calibrated propensity scores improve the speed of GWAS analysis by more than two-fold by enabling the use of simpler models that are faster to train.

2. 

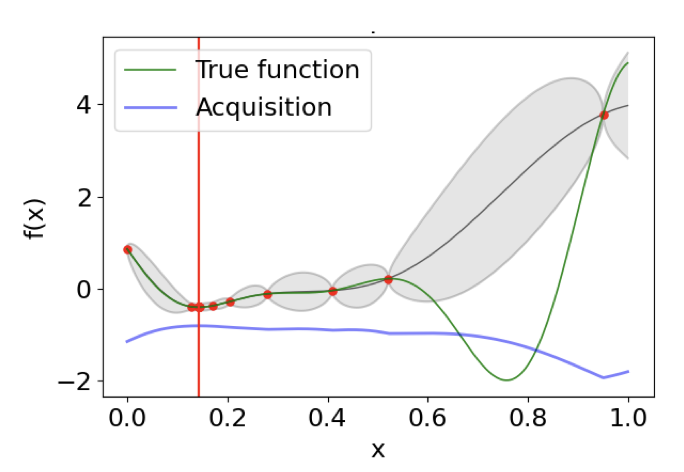   Online Calibrated and Conformal Prediction Improves Bayesian Optimization

   Shachi Deshpande, Charles Marx, and Volodymyr Kuleshov

   In Artificial Intelligence and Statistics (AISTATS) , 21–25 jul 2024

   Abs PDF

   Accurate uncertainty estimates are important in sequential model-based decision-making tasks such as Bayesian optimization. However, these estimates can be imperfect if the data violates assumptions made by the model (e.g., Gaussianity). This paper studies which uncertainties are needed in model-based decision-making and in Bayesian optimization, and argues that uncertainties can benefit from calibration – i.e., an 80% predictive interval should contain the true outcome 80% of the time. Maintaining calibration, however, can be challenging when the data is non-stationary and depends on our actions. We propose using simple algorithms based on online learning to provably maintain calibration on non-i.i.d. data, and we show how to integrate these algorithms in Bayesian optimization with minimal overhead. Empirically, we find that calibrated Bayesian optimization converges to better optima in fewer steps, and we demonstrate improved performance on standard benchmark functions and hyperparameter optimization tasks.

2022

1. 

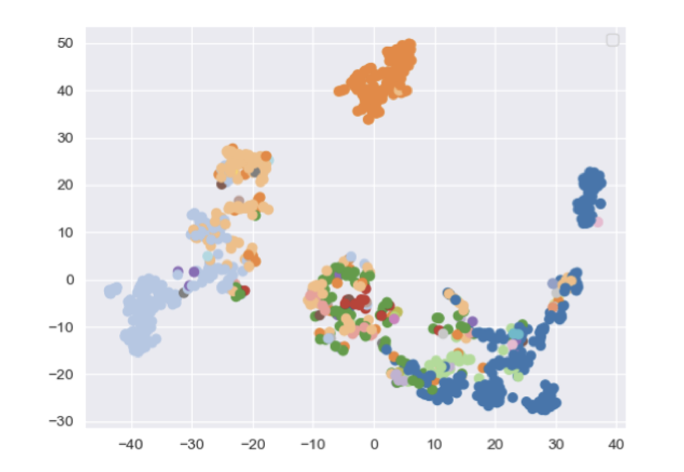   Deep Multi-Modal Structural Equations For Causal Effect Estimation With Unstructured Proxies

   Shachi Deshpande, Kaiwen Wang, Dhruv Sreenivas, and 2 more authors

   In Advances in Neural Information Processing Systems , 21–25 jul 2022

   Abs PDF

   Estimating the effect of intervention from observational data while accounting for confounding variables is a key task in causal inference. Oftentimes, the confounders are unobserved, but we have access to large amounts of additional unstructured data (images, text) that contain valuable proxy signal about the missing confounders. This paper argues that leveraging this unstructured data can greatly improve the accuracy of causal effect estimation. Specifically, we introduce deep multi-modal structural equations, a generative model for causal effect estimation in which confounders are latent variables and unstructured data are proxy variables. This model supports multiple multi-modal proxies (images, text) as well as missing data. We empirically demonstrate that our approach outperforms existing methods based on propensity scores and corrects for confounding using unstructured inputs on tasks in genomics and healthcare. Our methods can potentially support the use of large amounts of data that were previously not used in causal inference

2. 

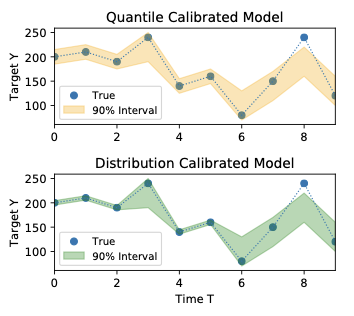   Calibrated and Sharp Uncertainties in Deep Learning via Density Estimation

   Volodymyr Kuleshov, and Shachi Deshpande

   In International Conference on Machine Learning, ICML 2022, 17-23 July 2022, Baltimore, Maryland, USA , 21–25 jul 2022

   Abs PDF

   Accurate probabilistic predictions can be characterized by two properties – calibration and sharpness. However, standard maximum likelihood training yields models that are poorly calibrated and thus inaccurate – a 90% confidence interval typically does not contain the true outcome 90% of the time. This paper argues that calibration is important in practice and is easy to maintain by performing low-dimensional density estimation. We introduce a simple training procedure based on recalibration that yields calibrated models without sacrificing overall performance; unlike previous approaches, ours ensures the most general property of distribution calibration and applies to any model, including neural networks. We formally prove the correctness of our procedure assuming that we can estimate densities in low dimensions and we establish uniform convergence bounds. Our results yield empirical performance improvements on linear and deep Bayesian models and suggest that calibration should be increasingly leveraged across machine learning.

2017

1. 

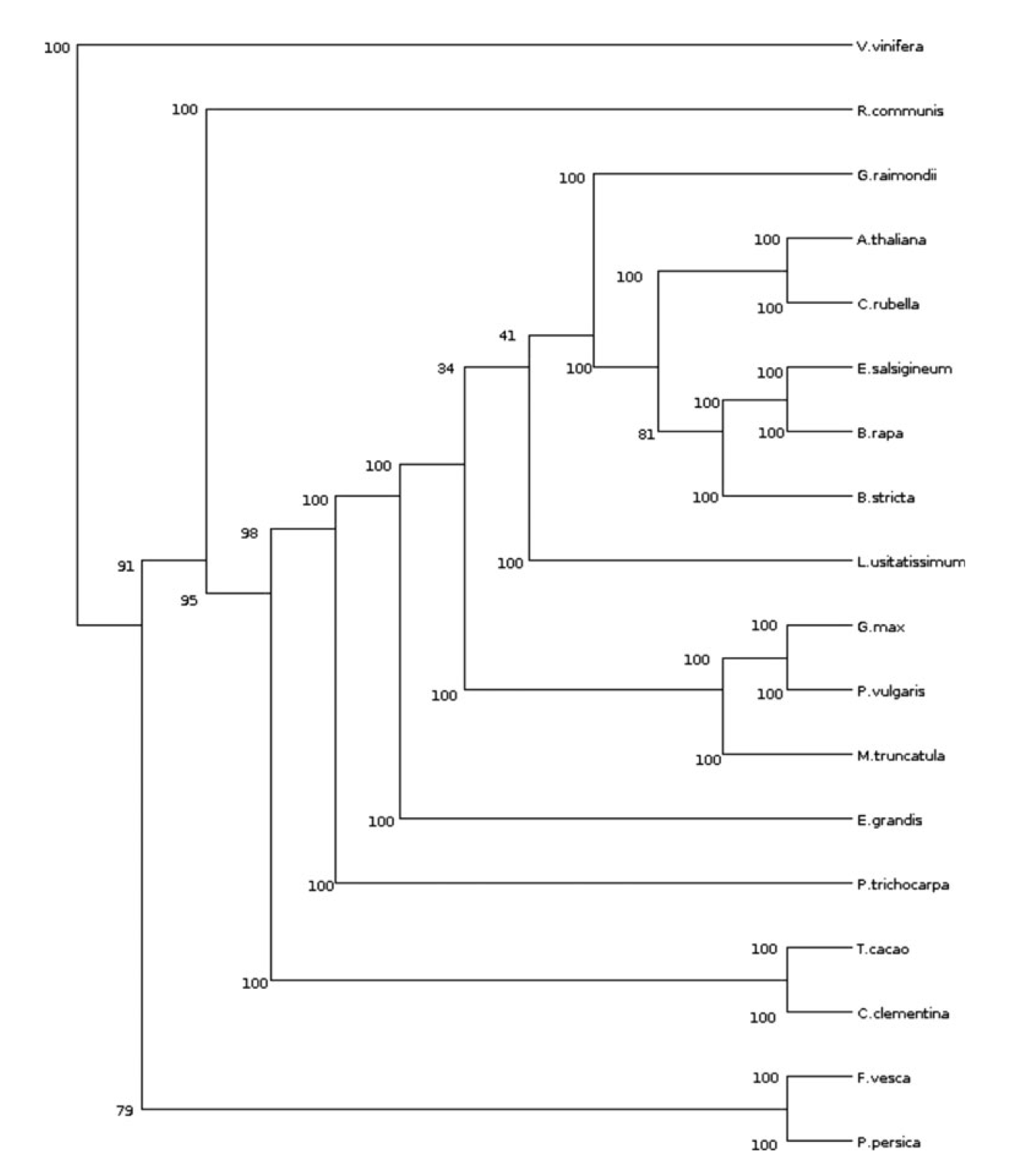   New Genome Similarity Measures based on Conserved Gene Adjacencies

   Daniel Doerr, Luis Antonio Brasil Kowada, Eloi Araujo, and 4 more authors

   J. Comput. Biol., 21–25 jul 2017

   Abs PDF

   Many important questions in molecular biology, evolution, and biomedicine can be addressed by comparative genomic approaches. One of the basic tasks when comparing genomes is the definition of measures of similarity (or dissimilarity) between two genomes, for example, to elucidate the phylogenetic relationships between species. The power of different genome comparison methods varies with the underlying formal model of a genome. The simplest models impose the strong restriction that each genome under study must contain the same genes, each in exactly one copy. More realistic models allow several copies of a gene in a genome. One speaks of gene families, and comparative genomic methods that allow this kind of input are called gene family-based. The most powerful-but also most complex-models avoid this preprocessing of the input data and instead integrate the family assignment within the comparative analysis. Such methods are called gene family-free. In this article, we study an intermediate approach between family-based and family-free genomic similarity measures. Introducing this simpler model, called gene connections, we focus on the combinatorial aspects of gene family-free genome comparison. While in most cases, the computational costs to the general family-free case are the same, we also find an instance where the gene connections model has lower complexity. Within the gene connections model, we define three variants of genomic similarity measures that have different expression powers. We give polynomial-time algorithms for two of them, while we show NP-hardness for the third, most powerful one. We also generalize the measures and algorithms to make them more robust against recent local disruptions in gene order. Our theoretical findings are supported by experimental results, proving the applicability and performance of our newly defined similarity measures.